MEFANET Journal 2014; 2(1): 10-14
ORIGINAL ARTICLE
Physiology in Modelica
Marek Mateják
Institute of Pathological Physiology, 1st Faculty of Medicine, Charles University in Prague, Czech Republic
* Corresponding author: marek@matfyz.cz
Abstract
Article history:
Received 7 March 2014
Revised 29 April 2014
Accepted 30 April 2014
Available online 12 May 2014
Peer review:
Stephen Randall Thomas, Michal Jurajda
Download PDF
Supplementary material
Modelica is an object-oriented language, in which models can be created and graphically represented by connecting instances of classes from libraries. These connections are not only assignments of values; they can also represent acausal equality. Even more, they can model Kirchhoff’s laws of circuits. In Modelica it is possible to develop library classes which are an analogy of electrical circuit components. The result of our work in this field is Physiolibrary (www.physiolibrary.org) – a free, open-source Modelica library for human physiology. By graphical joining instances of Physiolibrary classes, user can create models of cardiovascular circulation, thermoregulation, metabolic processes, nutrient distribution, gas transport, electrolyte regulation, water distribution, hormonal regulation and pharmacological regulation. After simple setting of the parameters, the models are ready to simulate. After simulation, the user can examine variables as their values change over time. Representing the model as a diagram has also great educational advantages, because students are able to better understand physical principles when they see them modeled graphically.
Keywords
Modelica library; physiology; integrative physiology; system biology; physiolibrary
Introduction
Guyton's model from 1972 [1] was our first model implemented using Modelica diagrams [2]. We immediately saw that the Modelica language has big potential in physiology. Further, we implemented huge models such as DigitalHuman/QHP and HumMod [3-7]. The result of abstracting these implementations is Physiolibrary [8], a freely-accessible Modelica library. Using Physiolibrary (www.physiolibrary.org) it is possible to very quickly write huge models in a nice graphical way. Physiological diagrams in the chemical / hydraulic / thermal / osmotic domain are similar to electrical diagrams. Connections generate equations according to Kirchhoff's laws. The sum of generalized flows (molar / volumetric / thermal) is zero, and generalized efforts (concentration / pressure / temperature) are equal in connections [9]. Each physical law can be described by just one class in the library. Please note that “class” here means the actual definition of the physical law, while “instance” means the one parameterized entity of this definition, as is usual in object-oriented programming. For example, instances describing the aorta, pulmonary artery or systemic large vein can be defined by just one class for blood vessels.
Other Modelica models and libraries covering the biological domain preceded Physiolibrary [10-15]. Most notable is the BioChem library, which implements a large part of the SBML library in Modelica [12-16]. However, nobody has such wide support for integrative physiology in Modelica as we have today, although many teams and projects throughout the world deal with this formalization and integration of physiology without using Modelica, for example: Physiome [17], SBML [15,16], EuroPhysiome [18], VPH[19], CellML [20] etc.
Methods
Integrative physiology needs exact interfaces and terminology to interconnect parts accurately. Primitive data types must be physical quantities with physical units. Above the quantities, the programmer must define physical connectors, and above the connectors library classes must be built, which are based on physical laws. From these elementary definitions in libraries, a user can build up more complex processes and regulations; and, finally, construct a whole-body physiological model. Because we use Modelica, it is not necessary to deal with the typical algebraic or numerical problems, since models are solved automatically. This allows building large models without huge effort.
In Physiolibrary (as in other correctly-defined Modelica libraries), all values are calculated in SI units only. This is really useful for compatibility with other libraries and models in case of integration. However, non-SI units are also integrated in some Modelica environments [8] (these units can be selected in parameter dialogs or in plotting of results).
The library structure is described in detail by Mateják [21]. The main packages are presented in the following sections.
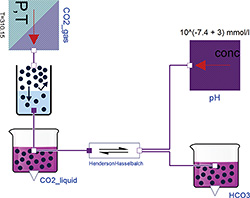
Figure 1: Henderson-Hasselbalch reaction in ideally buffered solution, where the Chemical classes GasSolubility, ChemicalReaction, Substance, UnlinitedGasStorage and UnlimitedSolution are used to build the model.
Figure 2: Cardiovascular part of Guyton, Coleman and Granger's model from 1972 [1], where the Hydraulic classes ElasticVessel, Conductor, Pump and PressureMeasure are used together with the cubic spline interpolation of a Starling curve.
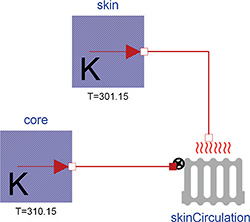
Figure 3: Heat losses from body core to skin, where the Thermal class IdealRadiator connects constant temperature sources represented by the class UnlimitedHeat.
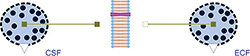
Figure 4: Osmotic example simulating liquid transfer between extracellular fluid and cerebrospinal fluid, which may cause a cerebral edema. The Osmotic classes OsmoticCell and Membrane are used.
Figure 5: SimpleReaction diagram
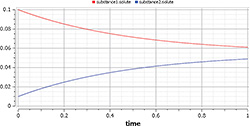
Figure 6: Results of SimpleReaction simulation
Chemical package
The main class from “Physiolibrary.Chemical” package is called "Substance". It has one chemical connector, where molar concentration and molar flow is presented as usually. An amount of a substance ("solute") is accumulated by molar flow inside an instance of this class. In the default setting the solvent volume is set to one liter, so in this setting the concentration at “mol/L” has the same value as the variable solute at “mol”. But in the advanced settings the default volume can be changed with external inputs. The molar flow at the port can be also negative, which means that the solute leaves the Substance instance. Most of the other chemical classes determine the molar flows from concentration gradients such as membrane diffusion, chemical reactions, Henry's law of gas solubility, chemical degradation or physiological clearance.
An idealized Henderson-Hasselbalch equation is presented here as an example of the Chemical package, see Figure 1. The fixed parameters in this example are: Henry's coefficient of CO2 (kH_T0=0.33 mmol/(L.kPa) at 25°C); the gas-liquid specific constant for Van't Hoff's temperature change (C=2400 K) for the GasSolubility instance; and the acid dissociation coefficient of the chemical reaction (Ka=10‑6.103 mol/L at 25°C). The enthalpy change (dH=15.13 J/mol) of this reaction can also be used to correct the dissociation coefficient for 37°C, but the correction is not significant in this case. All these fixed parameters are tabulated chemical values.
Other user inputs to this equation are the partial pressure of carbon dioxide in gas (pCO2) as a parameter of CO2_gas, and the activity of hydrogen ions as a parameter of the pH instance. Each parameter is always connected with one Physiolibrary class instance and can be viewed or set by clicking the instance. The outputs of this model are the amount of free dissolved carbon dioxide [CO2] and bicarbonate [HCO3-] in solution. For example, when pCO2=5.33 kPa, T=37°C and pH=7.4, the simulation can reach the equilibrium values [CO2]=1.24 mmol/L and [HCO3‑]=24.55 mmol/L. In reality it is not possible to hold pH constant for varying amounts of carbon dioxide. For real behavior with changing pH, the model must be extended with acid-base-buffers and electrolytes.
Hydraulic package
For modeling the cardio-vascular system, it is necessary to have support for basic hydraulics, and to have a connector that provides pressure and volumetric flow. Pressure can be generated by an elastic tissue surrounding some accumulated volume, as in the ElasticVessel class. Typically there is a threshold volume, below which the relative pressure is equal to external pressure and the wall of the blood vessels is not stressed. But if the volume rises above this value, the pressure increases proportionally. The slope in this pressure-volume characteristic is called “Compliance”.
Another way to generate the pressure is using a class that simulates the hydrostatic column. The hydrostatic pressure is proportional to height of the column. Between the two generated pressures a flow-generating class can be used, such as hydraulic resistance or hydraulic pump. An example model using the hydraulic package is Guyton's cardiovascular system [1] in Figure 2.
Thermal package
The "HeatAccumulation" library class models heat accumulation in Physiolibrary. This class has one thermal connector with temperature and heat flow. Heat energy is accumulated inside the class, stored in the variable "relativeHeat". This value is relative to normal body temperature of 37 °C; a positive value therefore indicates an internal temperature above 37 °C, while a negative value indicates temperature below 37 °C. Of course the particular value of temperature depends on the mass and specific heat of the instance.
In addition to heat convection or heat conduction the library also extends the Modelica Standard Library (MSL 3.2) with the IdealRadiator class. This class has two thermal connectors – one for liquid inside the radiator and another for the material around the radiator. Note that there is no liquid flow inside these connectors. The liquid flow can be described by a parameter or input to the instance. Together with the liquid specific heat, this flow determines the amount of heat flux from the liquid to a surrounding environment of different temperature. The calculation fulfills the ideal condition of microcirculation, where the outflowing blood has the same temperature as a tissue. This is really useful for modeling body thermal transfers, because the transfer of heat with blood flow is more significant than the typical rate of conduction through solid mass. Another example of its utility: the blood flow near the skin is regulated. This flow rate can affect how much heat leaves the body, especially in cold conditions. This is shown in Figure 3, where modeling constant temperatures of the body core (37°C) and skin (28°C), with a skin blood flow of 170 g/min and blood specific heat of 0.92 kcal/(kg.K), gives heat losses of about 1.4 kcal/min.
Osmotic package
To simulate the cell volume in hypertonic or hypotonic liquid, we use the classes from the Osmotic package. The main element is a semipermeable membrane, which generates the flow of penetrating substances together with water. The connector on both sides is composed of molar concentration of non-penetrating solutes (osmolarity), and from penetrating volumetric flow (osmotic flux). Flow through the membrane depends on a pressure gradient, where pressure on both sides is calculated from the osmotic and hydraulic component.
The liquid volume of the penetrating solution is accumulated in "OsmoticCell", where the nonpenetrating solutes are held. Instances of this class can represent both sides of the membrane, for example intracellular space, extracellular space, interstitial space, blood plasma or cerebrospinal fluid. An example model of the osmotic fluxes between extracellular fluid and cerebrospinal fluid is shown in Figure 4.
Usage example
Even though the Modelica language specification contains many pages (https://www.modelica.org/documents), creating models with Physiolibrary is simple. For example, imagine creating a model of the simple chemical reaction
A<->B. First we create a new model called "SimpleReaction" via the File menu. Then we drag the class Physiolibrary.Chemical.Components.ChemicalReaction out of the libraries browser, and drop it in our SimpleReaction diagram to create its instance in our model. In the same way, we also insert two instances of Physiolibrary.Chemical.Components.Substance. After that, we connect (by drawing a line with the mouse) the small square chemical connectors from the middle of the substance to the connectors of the chemical reaction. We just designed a model, shown in Figure 5.
After that we double-click the instance of the first substance, and use the parameter dialog to set its initial value to solute_start=0.01 mol. We do the same for the second substance, setting its initial value to solute_start=0.1 mol. For the reaction, we define dissociation as K=1 and set the forward reaction rate to kf=1 s-1.
Now we can simulate the model by just clicking the Simulate button. The results (Figure 6) of the simulation are accessible in Simulation or Plotting mode by selecting an option in the bottom-right corner of the environment.
If we examine the model in text mode, we can see that the following text representation is automatically generated from the graphically-developed model:
model SimpleReaction
Physiolibrary.Chemical.Components.Substance substance1(solute_start =0.01);
Physiolibrary.Chemical.Components.Substance substance2(solute_start = 0.1);
Physiolibrary.Chemical.Components.ChemicalReaction chemicalreaction1(K=1,kf = 1);
equation
connect(chemicalreaction1.products[1],substance1.q_out);
connect(substance2.q_out,chemicalreaction1.substrates[1]);
end SimpleReaction;
Looking at the relevant library classes we can see that each of them contains the chemical connector Physiolibrary.Chemical.Interfaces.ChemicalPort, with its molar concentration and molar flow. Instances of these connectors are being used as operands of the Modelica operator connect(), which during translation of the model automatically generates equality equations for the connected concentration, and for Kirchhoff's equation of zero-sum-of-flows for connected molar flows.
After the code is translated via the Modelica compiler, the compiler generates low-level code, where the following assignments describe the same model:
// Dynamics Section
substance1.q_out.conc := 1000.0*substance1.state;
substance2.q_out.conc := 1000.0*substance2.state;
chemicalReaction.rr := 0.001*(chemicalReaction.kf*((chemicalReaction.as[1]*
substance1.q_out.conc)^chemicalReaction.s[1]-(chemicalReaction.ap[1]*
substance2.q_out.conc)^chemicalReaction.p[1]/chemicalReaction.KaT));
der(substance1.state) := -chemicalReaction.rr*chemicalReaction.s[1];
der(substance2.state) := chemicalReaction.rr*chemicalReaction.p[1];
chemicalReaction.lossHeat := -chemicalReaction.dH*chemicalReaction.rr;
It is possible to see many other details in the translated code. For example, each parameter not assigned by the user is automatically set to its default value. For instance, “s” (stoichiometric coefficients of substrates), “p” (stoichiometric coefficients of products), “as” (activity coefficients of substrates) and “ap” (activity coefficients of products) are all set to one; while “dH” (reaction standard enthalpy change) is set to zero. And instead of “K” (the parameter value of the dissociation constant) the compiler uses the variable “KaT”, which may differs from “K” when the user also defines a nonzero value for “dH”.
Conclusion
Graphical modeling with Physiolibrary is very easy and intuitive. Using these physiological diagrams as a higher-level mathematical language is sufficient for describing the elementary physical processes of physiology. But these diagrams suffer the same limitations as electric diagrams. For example, the user must not directly connect instances of chemical substance, for the same reason as connecting two capacitors with different charges can cause a short circuit in the electric domain. In other words, both instances of a substance want to equalize their concentration without any resistance. To add a resistance some distribution class such as diffusion, chemical reaction, gas solubility or stream must be used.
Download the current version of Physiolibrary from www.physiolibrary.org, or from the Modelica website at www.modelica.org/libraries. After downloading and installing the Modelica environment, the library can be opened by, for example, loading its package.mo file. Today, Dymola is the best environment for Modelica, but there are also free alternatives such as OpenModelica (www.openmodelica.org), which indeed already integrates Physiolibrary (to access Physiolibrary in OpenModelica: from the OMEdit menu, select File > System Libraries). Another option for compiling and simulating the Modelica models is to use the textual environment JModelica. What is more, models created in Modelica can be translated into Functional Mock-up Unit (FMU), which has an open standardized Functional Mock-up Interface (FMI) supported by many simulation tools.
The Physiolibrary classes are implemented to give robust support for many use cases. Each class contains an equation for some physical law. The implementation is open-source, so everybody can see each equation behind each class. The purpose of Physiolibrary is to encapsulate the equations of elementary physical laws and to allow the user to build complex models. Since Physiolibrary models these complex equations graphically, a model will be readable by everybody. This graphical style is much more natural than the text-based code representation. These models could even be directly used for teaching students who have never seen Modelica before. The schematic model representations describe themselves, without needing to reference the underlying code.
But while the mathematical part of the work is made easy, each model still needs the correct parameters. Physiolibrary does not contain any default values for these inputs, but we are now developing a companion database and interface for known base physiological parameters. This project is called Physiovalues (www.physiovalues.org) and will also integrate many research results and measurements from third parties together with parameter identification, optimization and calibration algorithms [22].
Acknowledgments
This paper describes the outcome of research that has been accomplished as part of a research program funded by the Ministry of Industry and Trade of the Czech Republic via the grant FR—TI3/869; and by The Ministry of Education, Youth and Sports via the grant SVV-2014-260033.
In addition, the main author wants to thank Austin Schaefer for English language editing.
References
[1] Guyton AC, Coleman TG, Granger HJ. Circulation: overall regulation. Ann Rev Physiol 1972; 34(1): 13-44.
[2] Mateják M, Kofránek J, Rusz J. Akauzální" vzkříšení" Guytonova diagramu. Medsoft 2009: 105.
[3] Hester RL, Summers R, Iliescu R, Coleman TG. HumMod: a modeling environment for the simulation of integrative human physiology. Front Physiol 2011; 2: 12.
[4] Mateják M, Kofránek J. HumMod – Golem Edition – Rozsáhlý model fyziologických systémů. Medsoft 2011: 182-196.
[5] Mateják M, Kofránek J. Rozsáhlý model fyziologických regulací v Modelice. Medsoft 2010: 126-146.
[6] Kofránek J, Mateják M, Privitzer P. HumMod – large scale physiological model in Modelica. 8th International Modelica Conference 2011. Dresden, Germany.
[7] Kofránek J, Mateják M, Privitzer P, Tribula M, Kulhánek T, Šilar J, Pecinovský R. HumMod-Golem Edition: large scale model of integrative physiology for virtual patient simulators. World Congress in Computer Science 2013 (WORLDCOMP'13), International Conference on Modeling, Simulation and Visualisation Methods (MSV'13).
[8] Mateják M, Kulhánek T, Šilar J, Privitzer P, Ježek F, Kofránek J. Physiolibrary - Modelica library for Physiology. 10th International Modelica Conference 2014. Lund, Sweden.
[9] Kofránek J, Mateják M, Privitzer P, Tribula M. Causal or acausal modeling: labour for humans or labour for machines. Technical Computing Prague 2008: 1-16.
[10] Proß S, Bachmann B. An Advanced Environment for Hybrid Modeling and Parameter Identification of Biological Systems. 7th International Modelica Conference 2011.
[11] Cellier FE, Nebot A. Object-oriented Modeling in the Service of Medicine. 6th Asia Simulation Conference 2005.
[12] Nilsson EL, Fritzson P. BioChem-A Biological and Chemical Library for Modelica. 3rd International Modelica Conference 2003. Linköping, Sweden.
[13] Nilsson EL, Fritzson P. Biochemical and metabolic modeling and simulation with Modelica. BioMedSim 2005. Linköping, Sweden.
[14] Nilsson EL, Fritzson P. A Metabolic Specialization of a General Purpose Modelica Library for Biological and Biochemical Systems. 4th International Modelica Conference 2005.
[15] Brugård J, Hedberg D, Cascante M, Cedersund G, Gómez-Garrido À, Maier D, Nyman E, Selivanov V, Strålfors P. Biomax Informatics, AG. Creating a Bridge between Modelica and the Systems Biology Community. 7th International Modelica Conference2009. Como, Italy.
[16] Hucka M, Finney A, Sauro H, Bolouri H, Doyle JC, Kitano H, Arkin AP, Bornstein BJ, Bray D, Cornish-Bowden A. The systems biology markup language (SBML): a medium for representation and exchange of biochemical network models. Bioinformatics 2003; 19(4): 524-531.
[17] Bassingthwaighte JB. Strategies for the physiome project. Ann Biomed Eng 2000; 28(8): 1043-1058.
[18] Fenner JW, Brook B, Clapworthy G, Coveney PV, Feipel V, Gregersen H, Hose DR, Kohl P, Lawford P, McCormack KM. The EuroPhysiome, STEP and a roadmap for the virtual physiological human. Philos Trans R Soc A-Math Phys Eng Sci 2008; 366(1878): 2979-2999.
[19] Hunter PJ, Viceconti M. The VPH-physiome project: standards and tools for multiscale modeling in clinical applications., IEEE Rev Biomed Eng 2009; 2: 40-53.
[20] Smith L, Butterworth E, Bassingthwaighte JB, Sauro H. SBML and CellML translation in Antimony and JSim. Bioinformatics 2014; 30(7): 903-907.
[21] Mateják M. Physiolibrary - fyziológia v Modelice. Medsoft 2014.
[22] Kulhánek T, Mateják M, Šilar J, Kofránek J. Identifikace fyziologických systémů. Medsoft 2014: 148-153.
Supplementary material
Physiolibrary-2.1.0 (ZIP file, 9,38 MB)
Please cite as:
Mateják M. Physiology in Modelica. MEFANET Journal 2014; 2(1): 10-14. Available at WWW: http://mj.mefanet.cz/mj-03140307.
This is an open-access article distributed under the terms of the Creative Commons Attribution-NonCommercial-ShareAlike 3.0 License (http://creativecommons.org/licenses/by-nc-sa/3.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work, first published in the MEFANET Journal, is properly cited. The complete bibliographic information, a link to the original publication on http://www.mj.mefanet.cz/, as well as this copyright and license information must be included.
![Figure 2: Cardiovascular part of Guyton, Coleman and Granger's model from 1972 [1], where the Hydraulic classes ElasticVessel, Conductor, Pump and PressureMeasure are used together with the cubic spline interpolation of a Starling curve. Figure 2: Cardiovascular part of Guyton, Coleman and Granger's model from 1972 [1], where the Hydraulic classes ElasticVessel, Conductor, Pump and PressureMeasure are used together with the cubic spline interpolation of a Starling curve.](/res/image/vol2-iss1/03140307-fig02-thumb.jpg)